SDEV120: Abstract Syntax Trees

Tree Structures

A tree structure is a data structure that represents a hierarchy of elements. They are used in many areas of computer science.

In the previous lecture we discussed expressions. Computers need an algorithm to evaluate expressions. One way to do this is with a tree structure.

There are many algorithms for determining the order in which to visit nodes in a tree.

We will use a post-order traversal for syntax trees:

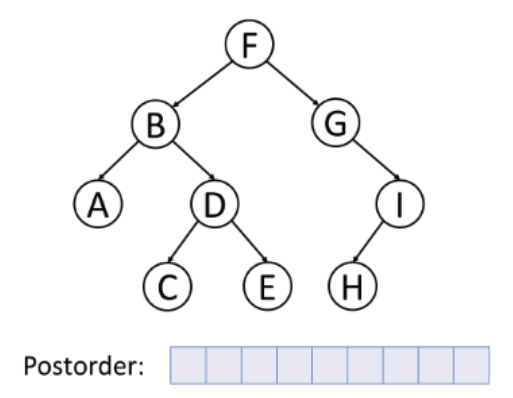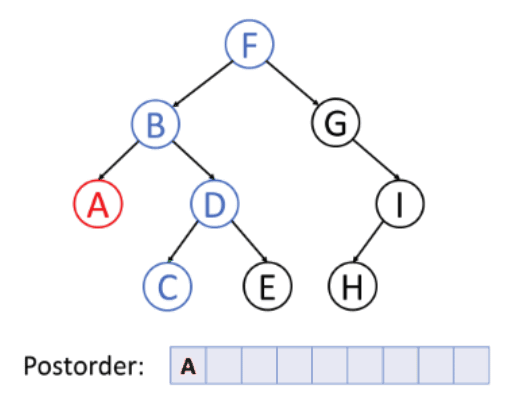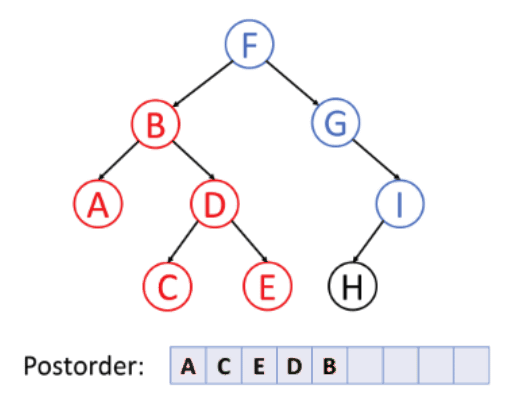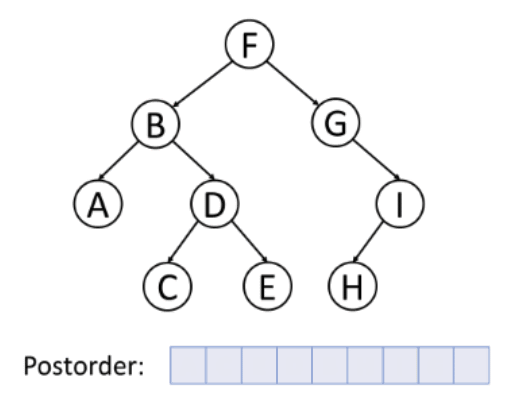
post-order tree traversal

In the graphic above, visits are shown in blue, evaluations in red.

Each leaf node (A, C, E, H) would be some operand, and each internal node (B, D, F, G, I) would be some operator.

An abstract syntax tree is a visual representation of the syntax of a programming language for some expression.

Below is a syntax tree containing literals and operators for the expression:

(7 + 3) * (5 - 2)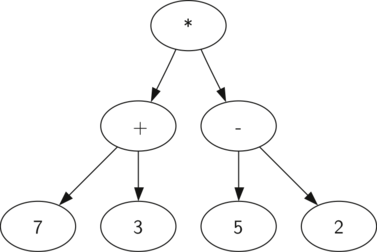

Draw the syntax tree for the following expressions:

1) 5 + 3 * 2

2) (5 + 3) * 2

3)  10 / 2 / 2 - 1

4)  10 / (2 / 2) - 1

If a syntax tree includes variables, we treat them just like literals.

(7 + x) * (y - 2)

We may need to substitute the function call with its definition within the tree. We just drop it in place.

Given the function:

f(x) = x / 2

Find the syntax tree for the following expressions:

1) 10 * f(4) + 3

2) 10 * f(y) + 3

3) f(2) * f(3)

Function Composition is the process of combining two or more functions to produce a new function.

Given the functions:

f(x) = x + 1
g(x) = x * 2

An example of function composition is f(g(x)).

We can use an AST for each function expression, then combine them into larger expressions:

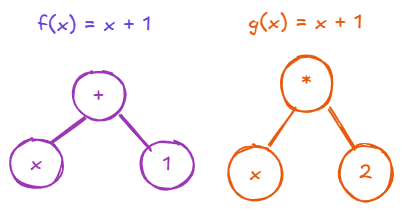
With function composition, the "x" in one function will be replaced by a whole function expression.

Given the functions:

f(x) = x + 1
g(x) = x * 2

f( g( 3 ) )
  = f( 3 * 2 )
  = f( 6 )
  = 6 + 1
  = 7

Given the functions:

f(x) = x + 1
g(x) = x * 2

1) g( f(3) )

2) f( f(2) )

3) f( f( f(6) + 1 ) + 2 ) + 3

Functions can take multiple arguments. In this case, we plug in the values for each argument in the order they are given.

Given the function:

f(x, y) = x + y + 1

Evaluate the following expressions:

1) f(3, 4)

2) f(1, 2)

3) f(3, f(2, 1))

We can drop in True and False values into our syntax trees along with logical connectives.

They work the same as we've seen so far.

Draw the syntax tree for the following expressions, evaluating them as you go:

1) True and False or False

2) True and (False or False)

3) not True